
The cut shown above makes it easy to see that the base length is unchanged. (As before, “height” is measured perpendicular to the base, and “base” is whichever side you chose first. Because base × height gives the area of the rectangle, we can use the same measurements on the parallelogram to compute its area: base × height. We can see that they also have exactly the same base length (blue) and exactly the same height (green). (See the definition of area for more about why those areas are the same.) Because the parallelogram and rectangle are composed of the same parts, they necessarily have the same area. We can figure out a formula for the area of a parallelogram by dissecting the parallelogram and rearranging the parts to make a rectangle. To include all numbers, we define the area of a rectangle to be base × height (where “base” and “height” mean the lengths of those sides, measured in the same units). (The pink parts show the completion of each square area-unit.) If we choose the corresponding square as our area-unit, we see that the blue rectangle contains five half-units of area and one quarter-unit of area, or a total of two and three-quarter units of area.
The blue rectangle shown here measures one-half length-unit high by five and one-half length-units wide.

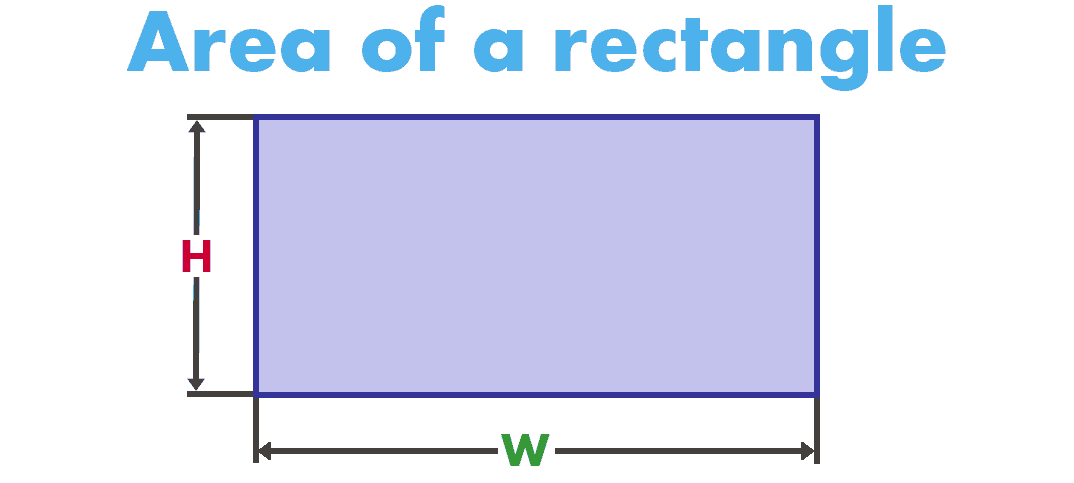
So the area is length × height.īecause a rectangle can be drawn at a slant, “height” is defined to mean “the direction perpendicular to the base,” and “base” is defined to be, well, whatever side you choose it to be. The number of rows is the height of the rectangle. The number of squares in one row is the length of the rectangle. Similarly, has 3 rows of 7 squares (or 7 columns of 3 squares), for a total of 7 × 3 squares, so its area is 21 square units. We can count the two rows of seven squares. If we decide that the area of this square is 1, then a rectangle that is 7 times as long would have 7 × 1 as its area.Ī rectangle that is twice the height of would have twice its area, so the area of is 2 × 7 units of area. (See also surface area.) Area of rectanglesīy choosing a square as the unit of area, we get an intuitive idea about the area of rectangles. Each formula they reinvent helps strengthen their understanding (and memory) for the other formulas they know. Students who have the informal notion that area is the “amount of 2-D ‘stuff'” contained inside a region can invent for themselves most of the formulas that they are often asked merely to memorize.


 0 kommentar(er)
0 kommentar(er)
